いまどきな見た目で描画するためのテクニックとして、PBRとIBLを使った間接光は重要です。教科書としては、最初は単純なLambertやPhongのシェーディングを学びます。しかしこれでは見劣りしてしまい、せっかく3D描画を出来るようになったのに感動が薄れてしまいます。勉強や挑戦を続けて行くためのモチベーションを維持するためにも、良い感じの見た目はある程度ほしいと私も感じます。
ということで、以前に書いた以下の記事のまとめとして本稿を書いています。ここでPBR (Physically Based Rendering) とIBL (Image Based Lighting) の話を完結させます。
はじめに
ここで PBR と IBL を扱っていくわけですが、実装にはいくつかのバリエーションが存在します。本記事では、glTF 2.0 で使用しているレンダリングを基準として取り扱っています。また、数式の詳しい背景情報は他のサイトが詳しく書かれているので、ここでは実装方面に注力した記事としています。
いまどきな見た目のためにはIBLも必要
直接光に対してPBRの方式で実装し、描画しても、物理ベースの雰囲気があまり感じられないのです。分かっている人がみれば、わかるものではあるのですが、最初に実装してみた体感としては、見た目の物足りなさを感じてしまいました。
いまどきの見た目を目指すのであれば、IBL を用いた間接光の影響を描画に取り入れる必要があります。
参考文献
いきなり説明を読んでも分からないことが多いかもしれません。私が学習した参考文献を先に紹介します。
Direct3D12ゲームグラフィックス実践ガイド
日本語でわかりやすい解説が書かれた書籍として、「Direct3D12 ゲームグラフィックス実践ガイド」があります。この書籍の「光伝達のモデル化」の章にある、間接光の計算の話は分かりやすいと私は感じます。
物理ベースレンダリングを柔らかく説明してみる(6)
PBRレンダリング周りでは、Qiitaのこちらの記事もよかったです。上記の本でわからないところをこちらで補ったり、その逆をやってみたりと活用できます。

Physically Based Rendering 第4版 日本語版
レンダリングをやる場合に、「Physically Based Rendering」の書籍を参考文献にあげる先輩方が多いように感じます。オリジナルは英語ですが、翻訳版も出ており、日本語で読むことができます。ただ、約1200ページのハードカバーでかなり分厚い本になっていて、読むのも大変です。
しかし、本当に基礎から始めて、ちゃんとした絵が出てくるということと、じっくり解説があるので、理解の段差が少ないことが挙げられます。とはいえ、モンテカルロ積分による推定の話は難しいと感じましたが。乱数を用いてレイトレーシングをする、マテリアルへの対処法を学ぶ、などはこの本によって、土台が出来てきたように思います。(が、本稿ではレイトレースで描画する話ではないので、そのあたりは触れずに進みます)
PBRとレンダリング方程式
PBRの根底にあるのは、光のエネルギー保存則と物理的に妥当な光の反射・吸収モデルです。これにより、マテリアルの質感や照明環境によらず、一貫した見た目を得ることができます。この土台になるのは、この分野ではおなじみのレンダリング方程式です。この式は以下のような形をしています。
$$
L_o(p, \omega_o) = L_e(p, \omega_o) + \int_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p, \omega_i) (\mathbf{n} \cdot \omega_i) d\omega_i
$$
- \(L_o(p, \omega_o)\) : \(\omega_o\) の方向への放射輝度
- \(L_e(p, \omega_o)\) : 自己発光している場合の \(\omega_o\)方向への放射輝度
- \(f_r(p, \omega_i, \omega_o)\) : BRDF(双方向反射率分布関数)であり、\(\omega_i\) の方向から \(\omega_o\) の方向へどれだけ光が反射されるか
- \( L_i(p, \omega_i) \): 入射光の放射輝度
- \(\mathbf{n} \cdot \omega_i\) : ランバートのコサイン項であり、光が表面に当たる角度による減衰を表します
ここでは自己発光を無しとして考えていきます。またこの積分はリアルタイムな描画では使えないため、以下の形の計算式を使います。これまでのシンプルなライティングで使用したことがある形に近いものになります。
$$
L_o=f_r(p, \omega_i, \omega_o) L_{color} (\vec{L} \cdot \vec{n})
$$
直接光: PBR ライティング
それでは直接光を対象として、PBRの実装をしていきます。先程のレンダリング方程式のうち、\(f_r(p, \omega_i, \omega_o)\) のBRDFを、以下のように分離して2つで実装します。
$$
f_r() = f_{diffuse}() + f_{specular}()
$$
\(f_{diffuse}\) は直接光のディフューズ成分、\(f_{specular}\)はスペキュラ成分です。
直接光: ディフューズ成分
ディフューズ成分は、光がマテリアル内部で散乱し、あらゆる方向へ均一に反射される非光沢な反射を表します。glTF 2.0では、多くの場合、Lambertian反射モデルが用いられます。また、メタリック・ラフネスフローを使用し、正規化ランバートでのBRDFは、以下の計算式となります。
$$ f_{diffuse} = \frac{baseColor.rgb \cdot (1-metallic)}{\pi}$$
- baseColor: ベースカラー
- metallic: メタルネスのパラメータ。非金属のとき0、金属のとき1.0となる
よって、直接光のディフューズ成分は、以下の計算式で実装します。
$$
C_{diffuse} = \frac{baseColor.rgb \cdot (1-metallic)}{\pi} \cdot L_{color} \cdot (\vec{L} \cdot \vec{n})
$$
直接光: スペキュラー成分
スペキュラ成分は、光沢のある反射を表し、主にマテリアル表面で反射される光です。glTF 2.0では、GGXマイクロファセットBRDFがよく使用されます。
スペキュラBRDFは、以下の3つの要素で構成されます。
$$
f_{specular} = \frac{D(h,\alpha)F(v,h)G(l,v,\alpha)}{4(\mathbf{n} \cdot \omega_i)(\mathbf{n} \cdot \omega_o)}
$$
- \(D(h)\): 法線分布関数(Normal Distribution Function – NDF)。マイクロファセットの法線が、ハーフベクトル h の方向を向いている確率
- \(F(v,h)\): フレネル項
- \(G(l, v, h)\): 幾何減衰項(Geometric Attenuation/Shadowing-Masking Function)
- h: ハーフベクトル
法線分布関数 (NDF)
GGXのNDFは以下のように定義されます。
$$
D(h) = \frac{\alpha^2}{\pi((n\cdot h)^2(\alpha^2-1)+1)^2}
$$
- \(\alpha\): 荒さ(ラフネス)パラメータから求まる値で、\(\alpha=roughness^2\) です
実装コードにすると、以下のようなものになります。
float D_GGX(float NoH, float alpha) { // NoH = max(dot(n,h), 0.0) とする
float alpha2 = alpha * alpha;
float NoH2 = NoH * NoH;
float denom = (NoH2 * (alpha2 - 1.0) + 1.0);
return alpha2 / (PI * denom * denom);
}フレネル項
Schlickの近似式がよく用いられます。
$$
F(v,h) = F_0 + (1-F_0)(1 – (v \cdot h))^5
$$
glTF 2.0では、メタリックパラメータとベースカラーによって以下の計算式で \(F_0\)を求めます。ここで、\(F_{0,dielectric}\)は、非金属のベース反射率で0.04を使用します。
$$
F_0 = lerp(F_{0,dielectric}, baseColor, metallic)
$$
幾何減衰項
GGXでは、SmithのG関数がよく使用され、ライト方向と視線方向の両方に対する減衰を考慮します。
$$
G(l,v,\alpha) = GGX_1(l, \alpha) GGX_1(v, \alpha)
$$
$$
GGX_1(v, \alpha) = \frac{2(n \cdot v)}{n\cdot v + \sqrt{\alpha^2 + (1-\alpha^2)(n \cdot v)^2} }
$$
計算結果
ここまでの計算をモデルに適用したものが以下の通りです。背景が映っていますがそれは考慮せず、別に与えた直接光から、モデルのライティングの計算をしています (ラフネスは 0.1 固定)。

間接光に取り組む
直接光をPBRで計算したにもか関わらず、先の結果は期待した見栄えに到達していないと感じられたのではないでしょうか。ただし従来のPhongのものと比べると、スペキュラハイライトの出方が、パラメータを変化させたときによくなっているハズです。
まだ期待した見栄えになっていない最大の理由は、間接光を考慮していないことでしょう。間接光を処理して、背景(環境)と馴染むレンダリングができると、おそらく期待した結果に近づくことでしょう。以前に説明を試みたのですが、私がゴールまでたどり着けませんでした。しかし今回は最後まで進めていきます。
環境マップの準備
周辺からの光の影響を受けるためには、環境マップが必要になります。この環境マップを元にライティングをしていくために、Image Based Lighting (IBL) と呼ばれます。ここで環境マップとして使用するデータは、各画素が8bitでは足りないので、HDR (High Dynamic Range)で記録された画像形式を使います。各所で公開されているものの多くは、.hdr 形式か、.exr 形式かといったところですが、このようなものを使用します。
データの入手
私がよく使用するのは、以下のサイトです。HDRで記録された緯度経度のパノラマ画像となっています。
パノラマからキューブマップへ
ベクトルを元にデータを参照したい都合から、環境マップをキューブマップ化します。多くの場合環境マップはパノラマ画像で提供されていることが多いためです。また、配布されている画像データが EXR 形式であるので、読み込みやすい形式へ変換も必要です。ツールで変換したいときには、NVIDIA Texture Tools Exporter を使うと狙った形式に変換しやすいかもしれません。
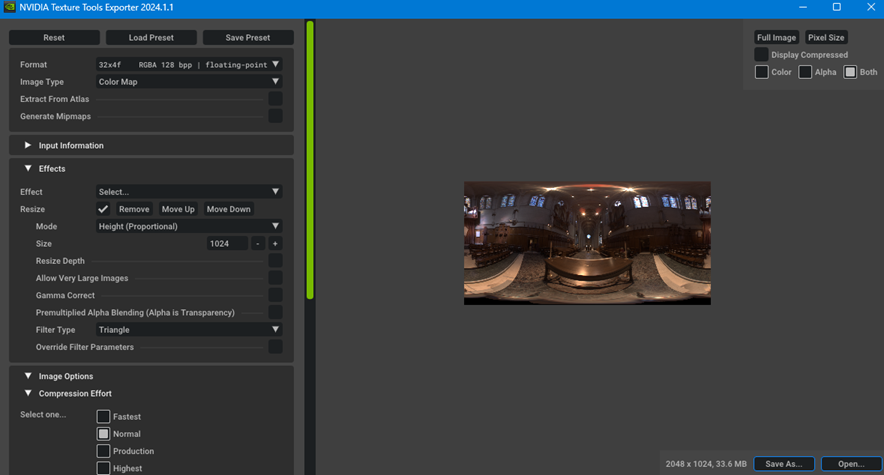
一般的には、EXRからDDS形式、もしくはHDR形式へ変換してDirectXTexで読み込み、その後キューブマップ化する、というのが多いのかもしれません。
環境マップをキューブマップ化して、この後の作業を進めます。

事前処理
間接光による描画の前に以下の事前処理が必要です。このデータを作成する処理を Prefilter 処理と呼ぶようです。
- ディフューズ用 IBL テクスチャ
- スペキュラー用 IBL テクスチャ
- GGX用 BRDF テクスチャ (LUT)
これらのテクスチャ作成、LUTテクスチャの作成では、レンダリング方程式をみながら、モンテカルロ積分を使い、重要度サンプリングによって基となる環境マップから生成するという手順となります。ただし、これらの作成に使用する計算式の導出については、本記事では省略します。私も参考にした、以下の2つの情報を参照してもらうのがよいと思います。かなり分かりやすいと思うのでお勧めです。

ディフューズ IBL テクスチャの作成
ディフューズ IBL テクスチャは、照度マップ (Irradiance map) とも呼ばれます。このテクスチャを作成するには、レンダリング方程式を以下のように変形し、積分は数値積分でおこないます。
$$
L_o(p, \omega_o) = k_d \frac{\rho}{\pi} \int_{\Omega} L_i(p, \omega_i) (\mathbf{n} \cdot \omega_i) d\omega_i
$$
積分の項が Irradiance を示し、半球からどれだけの光が到達しているかを示しています。ディフューズIBL テクスチャは、この Irradiance を事前に計算して格納しておく役割となっています。積分の項は厳密に求めることは難しいため、近似で求めます。モンテカルロ積分で求めることも出来ますが、処理負荷が高いので、多くの場合では重要度サンプリング(コサイン加重サンプリング)で処理されるようです。
$$
\int_{\Omega} L_i(p, \omega_i) (\mathbf{n} \cdot \omega_i) d\omega_i \approx \frac{1}{N}\sum_{i=1}^{N}\frac{L_i(\omega_i) (\mathbf{n} \cdot \omega_i)}{(\mathbf{n} \cdot \omega_i) / \pi}
$$
1点あたり2048回のサンプリングで作成した結果、以下のようになりました。

スペキュラ IBLのまえに、前提知識
ここでは、2013年にSiggraph でEpic Games が発表した手法を採用します。資料は以下のリンクで参照できるようです。
https://cdn2.unrealengine.com/Resources/files/2013SiggraphPresentationsNotes-26915738.pdf
リアルタイムレンダリングでは、環境マップからデータを取り出す回数には制約があります。そのため近似を使って可能な限り少ない回数で見た目とのバランスをとっていきます。
Split Sum Approximation という方法を用いて、以下のような計算2つに分解します。(この式は資料中のものを記載しているため、使用している文字の違いに注意してください)。近似した結果において、左側は光源に関する情報、右側はBRDFの情報(資料中では Environment BRDF)となっています。
$$
\frac{1}{N}\sum_{k=1}^{N}\frac{L_i(l_k)f(l_k,v)cos\theta_{l_{k}}}{p(l_k,v)} \approx \Big(\frac{1}{N}\sum_{k=1}^N L_i(l_k) \Big) \Big(\frac{1}{N}\sum_{k=1}^N\frac{f(l_k,v)cos\theta_{l_k}}{p(l_k,v)} \Big)
$$
この2つの項において、計算結果をテクスチャに事前に格納しておき、レンダリング時は参照して取り出して計算することで、スペキュラの結果を得ます。
スペキュラ IBL テクスチャの作成
スペキュラ用にIBLテクスチャは2つ用意します。先の式で登場した2つの項の計算結果を記録します。
PrefilteredEnvMap テクスチャの作成
以下の計算式で求まる部分をテクスチャに記録します。このテクスチャを Prefiltered Env Map と呼んだり、放射輝度マップと呼んだりします。このテクスチャの目的は、マイクロファセット理論に基づき、特定の粗さを持つ表面が、その環境から受け取るであろう平均的な鏡面反射光をシミュレートすることにあります。
$$
\Big(\frac{1}{N}\sum_{k=1}^N L_i(l_k) \Big)
$$
各テクセルに格納される値は、依然として光の輝度(Radiance)です。ただし、それは ある方向から見た、特定の粗さを持つ仮想的な表面が平均的に反射するであろう輝度を示すものです。
放射輝度マップの作成で使用するサンプリングの関数については、参考文献にあげたものが詳しいのでここで省略します。

テクスチャを作成し、ミップマップを切り替えながらアニメーションしたものが以下の通りです。

作成されたテクスチャのミップマップレベル1の様子が以下の通りです。

GGX BRDF LUT テクスチャの作成
続いて、下記に示される部分を計算するため、 BRDF LUTをテクスチャに記録します。ここでは視線と法線の角度、ラフネスパラメータを入力として計算ができるものになっています。書籍では DFG項と呼ばれている箇所になります。
$$
\Big(\frac{1}{N}\sum_{k=1}^N\frac{f(l_k,v)cos\theta_{l_k}}{p(l_k,v)} \Big)
$$
この式は、元の式との対応では以下の積分に相当します。第1項の \(F_0\)を除いた積分値をテクスチャのR成分に、第2項の積分をテクスチャのG成分に入れて LUT を作成したものが以下の図です。
$$
\int_{H}f(l,v)cos\theta_l dl = F_0 \int_{H}\frac{f(l,v)}{F(v,h)}(1 – (1 – v \cdot h)^5) + \int_{H}\frac{f(l,v)}{F(v,h)} (1-v \cdot h)^5 cos\theta_l dl
$$
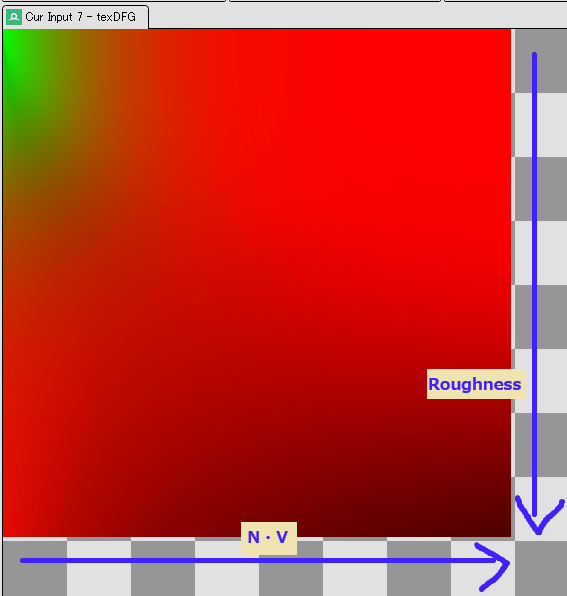
スペキュラーIBLを使って描画する
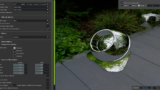
これまで作成したテクスチャを使用して、描画を行うと次の結果を得ることができます。ラフネスパラメータは 0.1固定で、左側はメタリックパラメータ=0、右側はメタリックパラメータ=1でモデルを描画したものです。

まとめ
ようやく今風の見た目をレンダリングするまでの流れについて記載できました。実装の詳細は触れていませんが、様々なところで実装されているのでそちらを見てみるのもよいでしょう。
個人的には、OpenGLやDirectXを用いて自力の3Dプログラミングを始めた人が、この描画を実装できるようになるまでの道のりは遠いと感じます。特にゴツイ数式(レンダリング方程式)が出てきたあたりで嫌悪感を感じてやめてしまう気がします。一方で、レイトレーシングから入ると、BRDFや確率的なレイ発射などへのベース知識があるため乗り越えやすいのかなと感じます。が、結局数学的な話がどこかに登場するので難しそうではあります。
最後に、ここまで到達したときの見栄えの良さはしっかり感じられるので、これから挑戦する人はめげずに頑張ってほしいと思います。
追記 (2025/11)
技術同人誌のイベント「技術書典19」にて、本件をまとめた冊子を作成・頒布しました。



コメント